Euclidean Sum of Squares Clustering Problems
Problem Description | Code | Results | Fisher's Iris Dataset | Ruspini's Dataset | German Towns (Spath) Dataset
Problem Description
Clustering (see, e.g. [Steinley 2006, Xu and Wunsch 2005]) is a fundamental problem in data analysis. Given a finite dataset
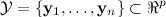
of n data points located in p-dimensional continuous space together with a second set of k points (aka cluster centers),
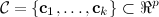
the clustering problem is to determine the positions of the cluster centers such that the mean sum of Euclidean distances (L2 Norm) between each data point and its nearest cluster center is minimized:
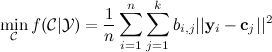
where
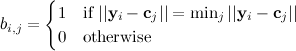
This is an unconstrained, continuous optimization problem of dimensionality kp. A candidate solution vector, x' can be represented by concatenating the p-dimensional coordinates of the cluster centers:
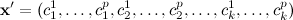
An instance of this problem type is uniquely specified by a dataset and choosing a value of k. For any problem instance,
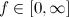
f=0 being the degenerate case when all data points are located exactly at one of the cluster centers. If the coordinates of each data point are finite, then a boundary (e.g. square) can be defined containing the dataset. This boundary implements an automatic penalisation on f; since no data points occur outside the boundary, f must increase monotonically if one or more cluster centers are moved outside and away from the boundary, with
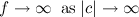
Note also that the value of f will only change when the "ownership" of one or more data points changes due to a movement of one or more cluster centres. This means that the solution vector can be changed without changing the value of f. Therefore, the fitness landscape consists of a very large number of flat regions and discrete transitions between them. The scale of this structure however depends on the data and k.
For algorithm benchmarking, it is useful to specify an initial search region in which the global optimum is located. For clustering problems, we can define a simple symmetric square boundary as
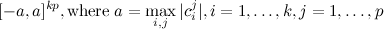
It may be possible to define a tighter initial search region, e.g. as a rectangular region using the range of the data points in each dimension. In any case these values are part of the problem specification.
Code
Some example Matlab code is provided here. No claims are made regarding the efficiency or elegance of this code!
- fitnessclustsse.m - This function implements the Euclidean sum of squares objective function for the clustering problems. Given: a dataset; value for k (the number of clusters); candidate solution vector. Returns: the objective function value.
- Usage example (requires data file german_postal.mat) - calculate fitness value of the global optimum for k=2:
>> load german_postal;
>> ggg = [722.944520639560e+000 95.9721033505540e+003 165.042584998811e+000 657.585035229536e+000 995.903499354406e+003 2.32154979550654e+003]';
>> fitnessclustsse(ggg,data)
ans =
6.025472220938822e+11
- Usage example (requires data file german_postal.mat) - calculate fitness value of the global optimum for k=2:
- cmaes_demo.m - A simple script that applies the Matlab implementation of CMA-ES (available here) to a set of problem instances using the German Towns/Postal data.
- Usage example (requires data file german_postal.mat):
>> cmaes_demo
- Usage example (requires data file german_postal.mat):
Results
A first set of results on these problem instances (using CMA-ES, Nelder-Mead simplex, random search and k-means) can be found in this paper:
- M. Gallagher. Clustering Problems for More Useful Benchmarking of Optimization Algorithms. To appear in Proc. Tenth International Conference on Simulated Evolution And Learning (SEAL 2014), 2014.
Problem Instance Families
Fisher's Iris Data
One of the most widely-used benchmark datasets in clustering is Fisher's Iris dataset [Fisher, 1936]. This dataset has 150 observations of 4 variables, i.e. n=150, p=4. k can be varied: since the data are observations of 3 species/classes of flowers, k=3 is one obvious choice, specifying a 12-dimensional optimization problem. The range of data values over all variables is [0.1,7.9] therefore we can define the initial search region as [0.1,7.9]^4k.
Dataset. In Matlab, the dataset is available ("load fisheriris"). Note that this is NOT identical to the UCI Machine Learning Repository version of the dataset [Bezdek et al., 1999].Problem Family Specification: <essclust,iris,(feasible bounds),(2pk)>
Instances
<essclust,iris,[0.1,7.9]^4,8> (k=2)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 152.347. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 152.347951760358
- Solution vector:
5.00566037735849 3.36981132075472 1.56037735849057 0.290566037735849
6.30103092783505 2.88659793814433 4.95876288659794 1.69587628865979
<essclust,iris,[0.1,7.9]^4,12> (k=3)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 78.8514. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 78.8514414261460
- Solution vector:
5.006000000000001 3.428000000000000 1.462000000000000 0.246000000000000
5.901612903225806 2.748387096774194 4.393548387096774 1.433870967741936
6.849999999999999 3.073684210526315 5.742105263157895 2.071052631578947
<essclust,iris,[0.1,7.9]^4,16> (k=4)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 57.2284. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 57.2284732142857
- Solution vector:
5.00600000000000 3.42800000000000 1.46200000000000 0.24600000000000
5.53214285714286 2.63571428571429 3.96071428571429 1.22857142857143
6.25250000000000 2.85500000000000 4.81500000000000 1.62500000000000
6.91250000000000 3.10000000000000 5.84687500000000 2.13125000000000
<essclust,iris,[0.1,7.9]^4,20> (k=5)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 46.4461. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 46.4461820512821
- Solution vector:
5.00600000000000 3.42800000000000 1.46200000000000 0.24600000000000
5.50800000000000 2.60000000000000 3.90800000000000 1.20400000000000
6.20769230769231 2.85384615384615 4.74615384615385 1.56410256410256
6.52916666666667 3.05833333333333 5.50833333333333 2.16250000000000
7.47500000000000 3.12500000000000 6.30000000000000 2.05000000000000
<essclust,iris,[0.1,7.9]^4,24> (k=6)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 39.0399. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 39.0399872460872
- Solution vector:
4.70454545454545 3.12272727272727 1.41363636363636 0.20000000000000
5.24285714285714 3.66785714285714 1.50000000000000 0.28214285714286
5.50800000000000 2.60000000000000 3.90800000000000 1.20400000000000
6.20769230769231 2.85384615384615 4.74615384615385 1.56410256410256
6.52916666666667 3.05833333333333 5.50833333333333 2.16250000000000
7.47500000000000 3.12500000000000 6.30000000000000 2.05000000000000
<essclust,iris,[0.1,7.9]^4,28> (k=7)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 34.2982. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 34.2982296650718
- Solution vector:
4.70454545454545 3.12272727272727 1.41363636363636 0.20000000000000
5.24285714285714 3.66785714285714 1.50000000000000 0.28214285714286
5.53214285714286 2.63571428571429 3.96071428571429 1.22857142857143
6.03684210526316 2.70526315789474 5.00000000000000 1.77894736842105
6.44210526315789 2.97894736842105 4.59473684210526 1.43157894736842
6.56818181818182 3.08636363636364 5.53636363636364 2.16363636363636
7.47500000000000 3.12500000000000 6.30000000000000 2.05000000000000
<essclust,iris,[0.1,7.9]^4,32> (k=8)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 29.9889. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 29.9889439507861
- Solution vector:
4.70454545454545 3.12272727272727 1.41363636363636 0.20000000000000
5.24285714285714 2.37142857142857 3.44285714285714 1.02857142857143
5.24285714285714 3.66785714285714 1.50000000000000 0.28214285714286
5.62857142857143 2.72380952380952 4.13333333333333 1.29523809523810
6.03684210526316 2.70526315789474 5.00000000000000 1.77894736842105
6.44210526315790 2.97894736842105 4.59473684210526 1.43157894736842
6.56818181818182 3.08636363636364 5.53636363636364 2.16363636363636
7.47500000000000 3.12500000000000 6.30000000000000 2.05000000000000
<essclust,iris,[0.1,7.9]^4,36> (k=9)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 27.7860. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 27.7860924173081
- Solution vector:
4.67894736842105 3.08421052631579 1.37894736842105 0.20000000000000
5.10000000000000 3.51304347826087 1.52608695652174 0.27391304347826
5.24285714285714 2.37142857142857 3.44285714285714 1.02857142857143
5.51250000000000 4.00000000000000 1.47500000000000 0.27500000000000
5.62857142857143 2.72380952380952 4.13333333333333 1.29523809523810
6.03684210526316 2.70526315789474 5.00000000000000 1.77894736842105
6.44210526315789 2.97894736842105 4.59473684210526 1.43157894736842
6.56818181818182 3.08636363636364 5.53636363636364 2.16363636363636
7.47500000000000 3.12500000000000 6.30000000000000 2.05000000000000
<essclust,iris,[0.1,7.9]^4,40> (k=10)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 25.8340. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 25.834054819972511
- Solution vector:
4.67894736842105 3.08421052631579 1.37894736842105 0.20000000000000
5.00000000000000 2.30000000000000 3.27500000000000 1.02500000000000
5.10000000000000 3.51304347826087 1.52608695652174 0.27391304347826
5.51250000000000 4.00000000000000 1.47500000000000 0.27500000000000
5.57647058823529 2.59411764705882 3.98235294117647 1.21764705882353
5.96875000000000 2.86250000000000 4.41250000000000 1.38125000000000
6.02777777777778 2.73333333333333 5.02777777777778 1.79444444444444
6.56818181818182 3.08636363636364 5.53636363636364 2.16363636363636
6.65454545454546 3.04545454545455 4.66363636363636 1.47272727272727
7.47500000000000 3.12500000000000 6.30000000000000 2.05000000000000
Ruspini's Data
This dataset has 75 observations of 2 variables, i.e. n=75, p=2. k can be varied. The range of data values over all variables is [4,156] therefore we can define the initial search region as [4,156]^2k.
Dataset (downloaded from the http://www.unc.edu/~rls/s754/data/ruspini.txt, 5/12/2013). The dataset is also available in R (cluster package).Problem Family Specification: <essclust,ruspini,(feasible bounds),(2pk)>
Instances
<essclust,ruspini,[4,156]^2,4> (k=2)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 89337.8. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 89337.832142857
- Solution vector:
41.0571428571429 45.4285714285714
66.9750000000000 132.800000000000
<essclust,ruspini,[4,156]^2,6> (k=3)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 51063.4. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 51063.4750456705
- Solution vector:
41.0571428571429 45.4285714285714
43.9130434782609 146.043478260870
98.1764705882353 114.882352941176
<essclust,ruspini,[4,156]^2,8> (k=4)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 12881.0. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 12881.0512361466
- Solution vector:
20.1500000000000 64.9500000000000
43.9130434782609 146.043478260870
68.9333333333333 19.4000000000000
98.1764705882353 114.882352941176
<essclust,ruspini,[4,156]^2,10> (k=5)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 10126.7. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 10126.7197881828
- Solution vector:
20.1500000000000 64.9500000000000
43.9130434782609 146.043478260870
68.9333333333333 19.4000000000000
80.5000000000000 100.250000000000
103.615384615385 119.384615384615
<essclust,ruspini,[4,156]^2,12> (k=6)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 8575.40. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 8575.40687645688
- Solution vector:
20.1500000000000 64.9500000000000
36.4166666666667 148.416666666667
52.0909090909091 143.454545454545
68.9333333333333 19.4000000000000
80.5000000000000 100.250000000000
103.615384615385 119.384615384615
<essclust,ruspini,[4,156]^2,14> (k=7)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 7126.19. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 7126.19854312354
- Solution vector:
20.0833333333333 58.0000000000000
20.2500000000000 75.3750000000000
36.4166666666667 148.416666666667
52.0909090909091 143.454545454545
68.9333333333333 19.4000000000000
80.5000000000000 100.250000000000
103.615384615385 119.384615384615
<essclust,ruspini,[4,156]^2,16> (k=8)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 6149.63. This is likely to be the following solution (obtained with an implementation of CMA-ES):
- Objective function value: 6149.639019314019
- Solution vector:
9.99999999539073 57.0000000911560
18.1250000429247 74.5000000049416
29.7142856868073 59.7142857449624
36.4166666574633 148.416666664583
52.0909090563180 143.454545495861
68.9333333537336 19.3999999830322
80.5000000304624 100.249999853326
103.615384611450 119.384615391991
<essclust,ruspini,[4,156]^2,18> (k=9)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 5181.65. This is likely to be the following solution (obtained with an implementation of CMA-ES):
- Objective function value: 5181.65183982684
- Solution vector:
9.99999995794373 57.0000000963804
18.1250000324401 74.4999999844186
29.7142856770504 59.7142857404662
36.4166666225643 148.416666701130
52.0909090595495 143.454545467191
68.9333332890974 19.3999999925601
79.0000000385553 95.3333332573537
95.3750000188838 121.375000071440
111.500000053734 116.000000093298
<essclust,ruspini,[4,156]^2,20> (k=10)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 4446.28. This is likely to be the following solution (obtained with an implementation of CMA-ES):
- Objective function value: 4446.28214285714
- Solution vector:
9.99999998451028 57.0000001197382
18.1249999519795 74.4999999628034
48.3999999868827 148.400000017397
111.499999946052 115.999999979363
29.7142856779033 59.7142857268467
78.9999999811306 95.3333332546766
95.3750000125771 121.375000025982
34.8999999082685 147.600000013715
68.9333334001723 19.3999999926389
58.9999997698014 133.000000271693
German Towns (Spath) Data
This dataset has 89 observations of 3 variables, i.e. n=89, p=3. k can be varied. The range of data values over all variables is [24.49,1306024] therefore we can define the initial search region as [24.49,1306024]^3k.
Dataset (downloaded from http://people.sc.fsu.edu/~jburkardt/datasets/spaeth2/spaeth2_07.txt, 3/9/2014).Problem Family Specification: <essclust,germantowns,(feasible bounds),(2pk)>
Instances
<essclust,germantowns,[24.49,1306024]^3,6> (k=2)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 6.02546e11. This is likely to be the following solution (obtained with an implementation of CMA-ES):
- Objective function value: 6.025472220938822e+11
- Solution vector:
657.585035229536e+000 995.903499354406e+003 2.32154979550654e+003
722.944520639560e+000 95.9721033505540e+003 165.042584998811e+000
<essclust,germantowns,[24.49,1306024]^3,9> (k=3)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 2.94506e11. This is likely to be the following solution (obtained with an implementation of CMA-ES):
- Objective function value: 2.94506562778027e+11
- Solution vector:
330.929873001869e+000 1.30602400169001e+006 3.94649962550106e+003
713.780501415945e+000 91.6535581591426e+003 163.365137450846e+000
1.24763537265257e+003 576.575000521688e+003 502.949702896911e+000
<essclust,germantowns,[24.49,1306024]^3,12> (k=4)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 1.04474e11. This is likely to be the following solution (obtained with an implementation of CMA-ES):
- Objective function value: 1.04474664100716e11
- Solution vector:
330.929743011785e+000 1.30602399951445e+006 3.94650004312708e+003
541.779866179642e+000 58.1246140071003e+003 156.899977893482e+000
1.05185106050775e+003 157.555275831868e+003 176.072345729327e+000
1.24763528729838e+003 576.574999890473e+003 502.949839416747e+000
<essclust,germantowns,[24.49,1306024]^3,15> (k=5)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 5.97615e10. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 5.97615267205269e10
- Solution vector:
330.929613274889e+000 1.30602399950604e+006 3.94649970137045e+003
495.780501388671e+000 51.4227550504051e+003 130.410264882195e+000
916.127773288099e+000 124.007071440605e+003 213.546517330764e+000
1.24763516914242e+003 576.575000286366e+003 502.950243522078e+000
1.27114572851323e+003 210.032555480127e+003 186.666483259584e+000
<essclust,germantowns,[24.49,1306024]^3,18> (k=6)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 3.59085e10. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 3.59085384380298e10
- Solution vector:
330.929200998046e+000 1.30602399948261e+006 3.94650038455577e+003
495.780409907402e+000 51.4227551216804e+003 130.410188360083e+000
916.127934385819e+000 124.007071422910e+003 213.546346185247e+000
984.240634772259e+000 685.782999989853e+003 696.598957973432e+000
1.27114552655582e+003 210.032555453881e+003 186.666559311675e+000
1.51102943023813e+003 467.367000019818e+003 309.300260613161e+000
<essclust,germantowns,[24.49,1306024]^3,21> (k=7)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 2.19832e10. This is likely to be the following solution (obtained with an implementation of k-means):
- Objective function value: 2.19832076153985e10
- Solution vector:
330.930708580577e+000 1.30602399953804e+006 3.94649967136739e+003
371.017004507240e+000 34.4121739158693e+003 141.343474666540e+000
607.209020766809e+000 70.1958666486647e+003 175.816655078203e+000
966.464957678033e+000 128.939875029566e+003 160.166594427141e+000
984.239249144631e+000 685.782999690448e+003 696.599796202028e+000
1.27114552974574e+003 210.032555399712e+003 186.666779664602e+000
1.51103013762400e+003 467.367000014776e+003 309.300342958735e+000
<essclust,germantowns,[24.49,1306024]^3,24> (k=8)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 1.33854e10. This is likely to be the following solution (obtained with an R clustering package (thanks Michael Banfield):
- Objective function value: 1.33854150525813e+10
- Solution vector:
330.930000000000e+000 1.30602400000000e+006 3.94650000000000e+003
363.336363636364e+000 33.6483636363636e+003 143.459090909091e+000
603.697777777778e+000 65.9055925925926e+003 119.777777777778e+000
861.246000000000e+000 107.830400000000e+003 235.840000000000e+000
984.240000000000e+000 685.783000000000e+003 696.600000000000e+000
1.04083400000000e+003 146.932666666667e+003 179.380000000000e+000
1.22295571428571e+003 220.149285714286e+003 204.428571428571e+000
1.51103000000000e+003 467.367000000000e+003 309.300000000000e+000
<essclust,germantowns,[24.49,1306024]^3,27> (k=9)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 7.80442e9. However subsequent papers in the literature (e.g. [Hansen et al., 2001; Bagirov 2008] use the value 8.42374e9. We assume this new value is the correct one (but if anyone can find a solution with the original value please let us know!) This is likely to be the following solution (obtained with CMA-ES):
- Objective function value: 8.423750573163314e+09
- Solution vector:
330.930024284082e+000 1.30602399997975e+006 3.94650004300091e+003
363.336349369481e+000 33.6483636658907e+003 143.459087237367e+000
603.697721603636e+000 65.9055926171194e+003 119.777835290498e+000
861.246060122426e+000 107.830400005495e+003 235.839999706162e+000
979.453074850298e+000 142.672461498681e+003 187.823090154207e+000
984.239855488777e+000 685.783000096644e+003 696.599980272967e+000
1.24088206632887e+003 186.151799958002e+003 170.839920559014e+000
1.30897497157283e+003 239.883499934192e+003 206.450087966198e+000
1.51103000771089e+003 467.367000004925e+003 309.299928740850e+000
<essclust,germantowns,[24.49,1306024]^3,30> (k=10)
- Global Optimum: the value of the global optimum is reported in [Du Merle et al., 2000] as 6.44647e9. This is likely to be the following solution (obtained with an R clustering package (thanks Michael Banfield):
- Objective function value: 6.44648364287013e+009
- Solution vector:
330.930000000000e+000 1.30602400000000e+006 3.94650000000000e+003
338.591000000000e+000 32.3351500000000e+003 150.105000000000e+000
534.996666666667e+000 56.2522666666667e+003 114.873333333333e+000
696.831875000000e+000 75.7002500000000e+003 119.662500000000e+000
866.603846153846e+000 110.421538461538e+003 252.915384615385e+000
979.453076923077e+000 142.672461538462e+003 187.823076923077e+000
984.240000000000e+000 685.783000000000e+003 696.600000000000e+000
1.24088200000000e+003 186.151800000000e+003 170.840000000000e+000
1.30897500000000e+003 239.883500000000e+003 206.450000000000e+000
1.51103000000000e+003 467.367000000000e+003 309.300000000000e+000
References
- Bagirov, A.M. (2008). Modified global k-means algorithm for minimum sum-of-squares clustering problems. Pattern Recognition 41(10), 3192-3199.
- Bezdek, J. C. and Keller, J. M. and Krishnapuram, R. and Kuncheva, L. I. and Pal, N. R. Will the real iris data please stand up?, IEEE Transactions on Fuzzy Systems 7(3):368-369, 1999.
- Du Merle, O., Hansen, P., Jaumard, B., & Mladenovic, N. (2000). An interior point algorithm for minimum sum-of-squares clustering. SIAM Journal on Scientific Computing, 21(4), 1485-1505.
- Fisher, R. A. (1936). The use of multiple measurements in taxonomic problems. Annals of eugenics, 7(2), 179-188.
- Hansen, P., Mladenovic, N. (2001). J-means: a new local search heuristic for minimum sum of squares clustering. Pattern recognition 34(2), 405-413.
- Steinley, D. (2006). K-means clustering: A half-century synthesis. British Journal of Mathematical and Statistical Psychology, 59(1), 1-34.
- Xu, R., & Wunsch, D. (2005). Survey of clustering algorithms. Neural Networks, IEEE Transactions on, 16(3), 645-678.
Up: Continuous Real-World-Representative Problem Repository
Last modified: 30/01/17. Marcus Gallagher